二、 光辐射(电磁波)的真实属性
——解惑经典力学与麦克斯韦方程组不相容的矛盾
要分析光辐射(电磁波)的真正属性,我觉得还是得靠经典力学的理论基础来探究。因为经典力学的理论基础是建立在人类战胜大自然的经验积累基础上的,是人类通过实践或实验而得出的认知经验累积的精髓,是通过人类与大自然的抗争而累积形成的经验之结晶。牛顿曾谦虚地说过:“他并没有多么伟大,他只是一个站在巨人肩膀上的人,比别人看得远一些罢了”。其实牛顿在这里指的“巨人”并不是代指“几个伟人”经验累积的意思,而是指“整个人类社会”经验累积的意思。
我们知道,逻辑推理方法是依随人类的主观意识而行事的,而大自然的演化运动规律则是客观现实的,是自然的一种存在形式。因此,当经典力学与麦克斯韦方程组产生不相容时,人类只能修正自己的逻辑推理方法,修改搀杂着主观思维形成的所谓科学理念,这样的做法是唯一的,是正确的,是不会错的。但是,在修改的过程中,我们一定要用实实在在的科学实践或实验和“自然存在”相接触,相碰撞,以此勘察清楚事物演化的来龙去脉,并要以这个事物演化的规律性、和逻辑性来推敲、来修正我们提出的科学理论,最起码的底线你也得在了解了事物演化的表象,由表及里地去探索事物自然存在的真相,否则就有可能产生用纯粹的人类主观意识编织起来的逻辑推理方法去创立、去干预、去修正大自然的演化运动规律,这可不是人类能修改得了的事!
至于经典力学与麦克斯韦方程组产生不相容事件,我们可以先用牛顿第一定律和第二定律来探讨光辐射(电磁波)的基本特性,然后通过宏观世界的科学实验来验证光辐射(电磁波)的基本特性。我想,这样应该能够解答清楚经典力学与麦克斯韦方程组不相容事件的真相。
(一)、惯性和动量
牛顿在他的力学第一定律里提出了惯性这个重要概念,而在第二定律里虽然只提及了力、质量和加速度这三个物理量之间的定量联系,但是,“惯性”这个物理特性充斥在整个牛顿第二定律里面。也就是说,是“惯性”使牛顿第二定律里的三个物理量之间产生了物理上的量化关系。
每个物体都有继续保持其静止或沿一直线作匀速运动的状态,除非有力施加于其上,迫使它改变这种状态,力是迫使物体改变静止或匀速直线运动状态的一种物理量。物体不仅在不受力时表现出“惯性”状态,在受力时也表现出惯性的状态。惯性是通过物体与物体之间的力的作用而获得的。力改变了物体能维持静止或匀速直线运动的惯性力,说白了,也就是改变了运动物体与参照系之间的移动演化状态,实质上,最最关键的也就是改变了运动物体的运动动量。因此,可以说,动量和惯性原本就是一回事——惯性是动量的化身,是物体遵守“动量守恒定律”而显现出来的表征。比如,看到一列匀速直线运动状态的火车(此时牵引力和阻力正好抵消,所以火车的牵引力在这里不予考虑),你可以说:根据惯性定义,这列列车在惯性系里作惯性运动;你也可以说:根据动量守恒定律,这列列车的运动状态完全是在恪守动量守恒定律。然而,现今的“科学人”不认为这一说法,非要钻牛顿先生提出的绝对时间、绝对空间的牛角尖,定要找出个绝对参照系来佐证牛顿先生的这一说法,因此,直到今天人们还没有搞清“惯性”的基本概念,竟弄出个“非惯性系”来扯淡。其实,这些人不是在找绝对参照系,而是在找“上帝”,想到“上帝”那儿问清楚,我们这个宇宙时空的由来,这好像有点不现实哦?实质上,我们这些宇宙精灵,只要知道时间和空间就足矣。也就是只要知道时间是用来计量事物(事件)演化过程的一种参数,而且时间参数是一种强制性的自然计量参数,而且,可以肯定地说,这种自然计量参数是绝对性的。宇宙中的一切物质都被“上帝”套上了时间这个枷锁。“上帝”给你时间,是监督你变化,监督你运动的;而给你一个空间(宇宙空间),是任由你在宇宙时空中翱翔,让你尽可能地发挥自己的所能。可想,在这样一个充满运动的宇宙时空中,怎么可能找得到绝对参照系,但是,你并不能因此来否定宇宙时空中的这些参数的绝对性。
惯性的属性究竟怎样?为了说明问题,我们不妨来做个更易理解的事例来分析。例如,我坐在一列火车车厢里,并且面朝火车前进的方向而坐。当火车在匀速直线运动时,我从袋子里摸出一粒玻璃小球放在光滑的桌面上,这时小球并没有从桌面上飞起向我坐的地方砸过来,而是停在桌面的某一点上动也不动;假设,这时我乘坐的火车车厢上面的顶棚是敞开的,并在火车要经过的隧道口上方安装—套机械装置,通过这个机械装置迅捷地给我面前的桌面上放上一粒玻璃小球的话,那不用说,这粒玻璃小球肯定会急速地朝我坐的方向砸过来,不知情的乘客以为这个玻璃小球着魔了,怎么会突然地飞射起来。其实非也,因为车厢外面投放进来的这粒玻璃小球并没有受到因火车的加速运动而施加给它的魔力,也就是火车没有施加给它一个与火车同等运动速度的运动量(或称为惯性),在没有与火车同等量的动量这个物理量的支持下,这粒玻璃小球肯定会急速地向我坐的方向飞射过来。其实这粒玻璃小球除地球引力之外,并没有受到别的运动力的作用,它之所以向我坐的方向飞射过来,完全是由于整个火车受到牵引力所维持的动量的作用而急速向前移动造成的。要说着魔,道是我从袋子里拿出来放在桌面上一动不动的玻璃小球着魔了,是被动量(或惯性力)施了魔法,也就是同车厢中的其它物质(包括车厢本身)一样,都被火车从开始启动时的加速运动施加了运动的动量(惯性)魔法。
在现实中,因为种种原因,火车的运行速度不可能一直保持相当稳定的匀速直线运动状态,而是有波动的。因此,我从袋子里拿出来放在桌面上的这粒玻璃小球,一定会随着火车的运行状态的变动而在光滑的桌面上前后左右地滚来滚去,这个现象产生的关键因素,就在于玻璃小球受外力作用的影响问题,也就是玻璃小球在桌面上的受力问题。由于玻璃小球的滚动性以及光滑桌面的摩擦系数小等因素的交叠作用,使得玻璃小球与桌面没有建立起很好的力的传导连接。由于玻璃小球与火车之间没有得到很好的力的传递连接,因此,从理论上来讲,玻璃小球受到来自桌面水平方向上的火车牵引力很小,可以说几乎为零,只有在碰到阻尼或障碍物时,才获得一些牵引力得以维持与车厢的动量(惯性)平衡。在桌面(理想化的,非常平整、光滑的桌面)上来回滚动时,可怜的玻璃小球仿佛只受到来自桌面对它的托力。也可以说,玻璃小球与运行中的火车没有建立起很好的动量上的转换(传递)连接,这就好像用一架匀速直线运动的直升飞机紧随在这节敞篷车厢的上空,并从直升机上垂下一件小物件悬挂在这个桌面上似的(这件悬挂物件与火车的力学关系和玻璃小球与火车的力学关系非常相似),并没有与火车有“力”的相互作用关系。当然了,确切来说,玻璃小球在桌面上不停地滚动这一物理现象,其实就是玻璃小球与火车的加速运动变化没有得到很好地“力”的衔接造成的,一旦玻璃小球动量的速度值与火车的运动速度存在差值,玻璃小球就会滚落到有阻挡物的地方,在受到阻挡的同时获得了与火车运动动量相平衡的运动动量,玻璃小球就是以这种方式与火车保持着运动力的关系。
扯了半天,惯性力的逻辑量化关系还没有作一个交代。不用说,根据前面的分析,可以肯定惯性力 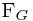 就是物体的质量
就是物体的质量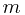 (考虑引力的话这里应该是重力)乘以该物体的运动速度
(考虑引力的话这里应该是重力)乘以该物体的运动速度 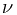 ,
,
即:  。
。
对了,物体的惯性力就等于物体的动量,只不过这里提到的动量是表征物体本身能继续移动的能力,对演化物体整个运行系统来说,这是一种既不含内能(质能)消耗又不受外力作用的运动能力,这种运动能力只能称它为“动量(或惯性)”。为什么说惯性力就是动量?因为在宇宙中,一切物体都保持有动量守恒的运动属性,有了动量守恒的运动属性,才能呈现出物体运动的动量演化特性,接着才能建有运动物体的运动连续性,随后才能拥有物体的机械运动的变化连续性。而惯性只不过是因物体的动量守恒运动而呈现出的一种物理表象,如果物体不遵守动量守恒定律(宇宙中没有真正的静止物体,只有相对的静止物体,因此,任何运动状态的物体都有动量,都在恪守动量守恒定律),也就不会向大自然呈现物体运动的惯性现象,那么,也就不会有“惯性”这个物理概念的存在。在宇宙中,因为有了动量才有了物体与物体之间的力的作用,而物体因遵守运动动量守恒才显示出了惯性的运动特性。也就是说,惯性是物体因遵守动量守恒法则而展示出的具体表现——是物体在加纳、维持、释放动量过程时的一种表观现象。因此可以说,惯性原本就是动量的影子,是动量的化身,它们的量化关系理应合而为一。实际上,质点的动量守恒定律也就是惯性定律,或称牛顿第一定律(为什么不把这一定律作进一步的推演拓展,我真有点想不明白)8。
作具体解析。例如,有一列匀速直线运动的火车,车上横向装有一个固定的L型挡板,在L型挡板的火车运行方向的一侧放上一粒玻璃小球。当火车来了个紧急刹车,这个玻璃小球肯定会沿着火车运行的方向继续向前运行而飞了出去(如果没有外力的干涉作用,这个玻璃小球肯定会不停地飞行着)。从理论上或观察表象上分析,刹车之后,这个玻璃小球根本就没有受到外力的作用,而是靠自身的内存动量(玻璃小球被火车牵引力带动而加有的运动动量)飞出去的。从地面上的角度观察思考,一个物体在没有外力和内力(内能力)的作用下能克服重力的影响而飞掷出去,这个动力别无他选,只能是惯性力,而这个惯性力的大小一定要满足:正好能举起这个玻璃小球的重量G(或质量 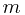 )以及玻璃小球飞出去的初速度
)以及玻璃小球飞出去的初速度 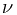 (火车紧急刹车前的运行速度)的条件。
(火车紧急刹车前的运行速度)的条件。
无可争辩,从上面这个例子就可以看出,动量和惯性力是同一个物理参数的两种说法。在任何参照系里,物体只要存有动量,并且一时无法传递给其它物体,它将保持其既有的动量使物体沿“直线运动方向”继续运动前行,直至转换给其他介质(物体),这就是宇宙物体的动量守恒法则,也是惯性的真正由来。例如:有一列高速运行的动车组列车行驶在上海至北京的干线上,由于发生事故,司机连忙启动紧急停车装置,但列车还是在钢轨上摩擦滑行了0.5公里左右才停了下来。针对列车在钢轨上滑行了0.5公里的问题,你可以这么说:根据惯性定义,物体在质量不变的情况下,其移动速度越快获得的惯性就越大,由于列车的质量 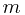 不仅大,而且运行速度
不仅大,而且运行速度 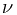 又非常的快,可想而知,其惯性是非常大的,如此巨大的惯性力,光靠轮子与钢轨之间的摩擦作用,要想在一瞬间的时间内消耗(转换)掉,那当然是不行的,非得要用一段作用时间(一段移动距离)来消耗(转换)掉如此大的惯性力;你还可以这样说:根据动量定义,物体在质量不变的情况下,其移动速度越快,获得的动量也就越大,而且动量是守恒的,不可能无缘无故地消失掉,在这个事故中,由于列车的质量
又非常的快,可想而知,其惯性是非常大的,如此巨大的惯性力,光靠轮子与钢轨之间的摩擦作用,要想在一瞬间的时间内消耗(转换)掉,那当然是不行的,非得要用一段作用时间(一段移动距离)来消耗(转换)掉如此大的惯性力;你还可以这样说:根据动量定义,物体在质量不变的情况下,其移动速度越快,获得的动量也就越大,而且动量是守恒的,不可能无缘无故地消失掉,在这个事故中,由于列车的质量 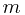 不仅大,而且运行速度
不仅大,而且运行速度 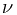 又非常快,可想而知,列车获得的动量是非常大的,如此巨大的动量光靠轮子与钢轨之间的摩擦作用,想在一瞬间的时间内转换掉,当然是行不通的,非得要用一段作用时间(一段移动距离)来转换掉如此巨大的运动动量。
又非常快,可想而知,列车获得的动量是非常大的,如此巨大的动量光靠轮子与钢轨之间的摩擦作用,想在一瞬间的时间内转换掉,当然是行不通的,非得要用一段作用时间(一段移动距离)来转换掉如此巨大的运动动量。
从动量(惯性)公式:  中,我们可以看出,当移动物体的质量不变时,动量(惯性力)的大小跟速度成正比,也就是速度愈快,物体的动量(惯性力)就愈大,速度渐慢,物体的动量(惯性力)也就渐小。而当移动物体的动量保持不变时(实质上也就是在,质量跟速度就成反比关系,也就是物体的质量越小,它获得的惯性运动速度就越快,物体的质量越大,它能获得的惯性运动速度就越慢。但是,质量与速度的反比关系仅适于物体在受到外力作用时(或受到动量冲击时的瞬间)才起作用。也就是物体在没有外力作用下,仅依靠惯性力来维持运动的情况下,其物体的质量
中,我们可以看出,当移动物体的质量不变时,动量(惯性力)的大小跟速度成正比,也就是速度愈快,物体的动量(惯性力)就愈大,速度渐慢,物体的动量(惯性力)也就渐小。而当移动物体的动量保持不变时(实质上也就是在,质量跟速度就成反比关系,也就是物体的质量越小,它获得的惯性运动速度就越快,物体的质量越大,它能获得的惯性运动速度就越慢。但是,质量与速度的反比关系仅适于物体在受到外力作用时(或受到动量冲击时的瞬间)才起作用。也就是物体在没有外力作用下,仅依靠惯性力来维持运动的情况下,其物体的质量 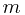 与速度
与速度 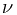 是不能成反比关系的。因为在惯性运动状态中,移动物体所获得的质量
是不能成反比关系的。因为在惯性运动状态中,移动物体所获得的质量 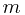 ,必定都是外来之物,而这些外来之物的自身必定带有动量,这些动量与移动物体的动量发生冲突必定产生力的作用——运动力学上称之为外力作用,可以说,这种外力作用(外来动量)的影响肯定是避免不了的。因而,在此种情况下,动量不变是不可能的。所以,在现实中,惯性运动物体的质量增加,其运动速度就会变慢的反比关系已被破坏而不能成立(质量增加,速度不一定变慢)。而当惯性运动物体的质量减少时,其运动速度顶多只能保持不变,而绝对不可能跟随变快。例如,在宇宙星际中旅行的星际物质——小行星。我们知道,小行星在围绕太阳运转的动力主要是依靠自身的动量(惯性力)在起作用(维持技撑着)。假如这个小行星在飞行中因某种原因而一分为二,分成两个小行星。对分裂后的单个小行星来说,质量是减少了许多,但是,它的运行速度还是基本不变的。因为从整个分裂过程来看,小行星在分裂过程中,它的原有总的动量(惯性力)没有得到增加,因此,分裂前与分裂后的总动量(惯性力)保持不变。再怎么说,根据动量守恒原则,这两颗小行星的运动速度也必定要保持不变。用数学公式表示:
,必定都是外来之物,而这些外来之物的自身必定带有动量,这些动量与移动物体的动量发生冲突必定产生力的作用——运动力学上称之为外力作用,可以说,这种外力作用(外来动量)的影响肯定是避免不了的。因而,在此种情况下,动量不变是不可能的。所以,在现实中,惯性运动物体的质量增加,其运动速度就会变慢的反比关系已被破坏而不能成立(质量增加,速度不一定变慢)。而当惯性运动物体的质量减少时,其运动速度顶多只能保持不变,而绝对不可能跟随变快。例如,在宇宙星际中旅行的星际物质——小行星。我们知道,小行星在围绕太阳运转的动力主要是依靠自身的动量(惯性力)在起作用(维持技撑着)。假如这个小行星在飞行中因某种原因而一分为二,分成两个小行星。对分裂后的单个小行星来说,质量是减少了许多,但是,它的运行速度还是基本不变的。因为从整个分裂过程来看,小行星在分裂过程中,它的原有总的动量(惯性力)没有得到增加,因此,分裂前与分裂后的总动量(惯性力)保持不变。再怎么说,根据动量守恒原则,这两颗小行星的运动速度也必定要保持不变。用数学公式表示:
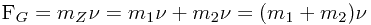 。
。
与此相类似的情况有很多,比如一个匀速直线运行的车厢,车厢的运行速度是每小时100公里,牵引力在拖动车厢作匀速直线运动时,是把车厢和车厢内的所有物品当作是一个整体物件而一起拖着跑的。当发生交通事故时,如车厢撞击在巨大障碍物时,车厢的移动速度从每小时100公里一下子降到近似于零。这时不考虑空气阻力的话,车厢上一切没有被阻挡、没有被牢牢固定住的物品或人,不管质量大小,肯定会以原有的运行速度一齐向车厢移动的方向飞出。这也是一种动量(惯性力)的分裂运动,这些分散的动量(惯性力)加起来就是本来以车厢为整体的总的动量(惯性力)。因此,在事故发生时,车厢里的物品和人向外抛出的惯性运动初速度是相同的,统一的。从上面这些分析可以看出,我们在探究自然事物时,一定要先了解清楚事物的自然运动的量化关系,然后才能踏实地运用数学这个逻辑运算工具进行逻辑性的运算分析,否则就会错误百出。
通过上述的探讨,可得出这样一个结论:物体的动量(惯性力)是通过物体与物体之间的动量(惯性力)的相互作用(转换)而获得的。物体在接受外界动量(惯性力)作用时的运动状态是动量(惯性)运动的临界状态(实质上也就是“输入”“输出”运动动量状态)。所谓的临界状态,其实就是:物体与外部有作用力(动量)的交换关系,而一旦脱离了与外力的作用关系,它就直接进入惯性的运动状态,也就是进入了严守动量守恒法则的运动状态。因此,物体的惯性运动速度跟物体刚脱离外力作用时的最初状态有关,也就是物体在惯性运动之初所拥有的运动速度就是物体脱离外力作用时所拥有的运动速度。而且惯性(动量)运动初始的运动速度将是整个惯性(动量)运动过程中的最高速度。为什么这么说,因为在任何惯性运动系统中,由于物体得不到外界动量的补充(在宇宙中,一个完全封闭的,一点不受外力影响的独立运动系统是不存在的),因而,不管移动物体的质量减少了多少,惯性移动物体的移动速度只会下降或免强保持不变,而绝对不可能会逐渐上升、或超过前面惯性运动伊始的初速度,除非有外力(或内部质能损耗而获得的推力)的干预。
再作进一步地分析。例如,有一架喷气式战斗机,飞机上的炮弹质量和整架飞机的质量虽然相去甚远,但飞机上的炮弹的动量(惯性)运动速度和整架飞机的运动速度却是同一个速度。当飞机在空战中开炮,炮弹从炮膛里发射时,它的飞行速度就要受到炮弹本身质量所拥有的动量(也就是炮弹在地球惯性系上所显现出的惯性作用力)的影响。如飞机的前置炮发射的炮弹,其最终获得的惯性(动量)飞行就等于炮弹受弹药爆炸得到的动量(瞬间冲击推力),再加上原本因炮弹搭载飞机而拥有的动量(自身质量与飞机运动速度而构成的惯性力);而用飞机尾炮向后方发射的炮弹(我想,现代超音速战斗机肯定已经不再安装向后发射的尾炮了),因弹药爆炸而获得的动量推力方向与原搭载飞机而获得的动量(惯性力)的运动方向是相反的,如此,炮弹最终获得的惯性飞行动量也就等于炮弹受弹药爆炸得到的动量(冲击推力)减去原本因炮弹搭载飞机而有的动量(惯性力)。上述的物理量化关系用公式表示:
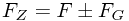 ,
,
其中  ,
, 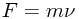 ,
, 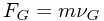 。
。
在  中,
中, 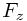 表示炮弹最终得到的动量(惯性力),
表示炮弹最终得到的动量(惯性力), 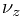 表示同时得到的最终惯性运动速度; 在
表示同时得到的最终惯性运动速度; 在 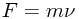 中,
中, 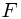 表示炮弹通过弹药这个外力的帮助而得到的惯性运行动量,
表示炮弹通过弹药这个外力的帮助而得到的惯性运行动量, 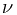 表示同时得到的惯性运行速度;在
表示同时得到的惯性运行速度;在 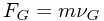 中 ,
中 , 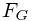 表示炮弹搭载飞机而应有的惯性力(动量),
表示炮弹搭载飞机而应有的惯性力(动量), 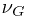 表示搭载而有的惯性运动速度(可以说就是飞机的飞行速度)。
表示搭载而有的惯性运动速度(可以说就是飞机的飞行速度)。
所以上式可写成: 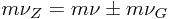
因在这个过程中炮弹的固有质量 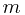 是保持不变的,
是保持不变的,
因此等式可转化为: 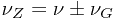 。
。
通过上面这个关系式可以看出,经典力学中的速度相加原理,其实就是大自然中的动量(惯性)相加原理的简化版。
说到这里,或许有人会提出这样的质疑:牛顿在经典力学第一定律里曾指出:“每个物体在不受外力作用时,都有一个保持其静止或沿一直线作等速运动状态”。牛顿在该书另一处还明确说明了“惯性”这一名词的涵义,指出:“它是每个物体按其一定的量而存在于其中的一种抵抗能力,这种抵抗能力使物体保持其原来的静止状态或者在一直线上等速运动的状态9”。也就是说,物体的惯性是安其一定的质量而存在于其中的一种抵抗能力,任何物体只要有质量,也一定就有惯性的存在,就是处在静止状态的物体也一定持有惯性力。而在我所提出的惯性就是动量的量化关系公式 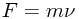 中,当物体的速度
中,当物体的速度 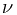 等于零时,该物体的惯性(或动量)也就等于零。也就是说,物体静止时是不存在动量(惯性力)的,此时物体的动量(惯性力)属性也就不复存在了?!这个质疑提得好!其实我这里所阐述的惯性力和惯性运动速度与牛顿提出的惯性定律基本是没有冲突性的。因为我们人类在衡量某一宇宙物体究竟是运动还是静止时,是相对某参照系(或参照物)而言的,而且在探测某个物体的动量(惯性力)大小时,也是相对与这个物体可能发生物理关系的参照系而言的。可以说,我提出的动量(惯性)的量化逻辑关系完全符合牛顿的经典力学。
等于零时,该物体的惯性(或动量)也就等于零。也就是说,物体静止时是不存在动量(惯性力)的,此时物体的动量(惯性力)属性也就不复存在了?!这个质疑提得好!其实我这里所阐述的惯性力和惯性运动速度与牛顿提出的惯性定律基本是没有冲突性的。因为我们人类在衡量某一宇宙物体究竟是运动还是静止时,是相对某参照系(或参照物)而言的,而且在探测某个物体的动量(惯性力)大小时,也是相对与这个物体可能发生物理关系的参照系而言的。可以说,我提出的动量(惯性)的量化逻辑关系完全符合牛顿的经典力学。
众所周知,在整个宇宙中,一切物质都得参与宇宙的演化运动,这是“上帝”的旨意。然而,宇宙中只要有演化运动的存在,就必定有位移(物体与物体之间最起码有基本粒子的位移运动)运动的存在,因而也就必定有量化关系的架构模式存在,位移运动构成物质的量化逻辑关系是宇宙演化运动的必然形式。可以说,在如此演化正酣的宇宙中,不可能存在真正的静止物体(或物质)。也因此可以这样分析认为:任何物体相对某个参照系或参照物而言是静止的,那只是相对这个参照系(或参照物)而言的,而这个参照系(或参照物)相对别的参照系肯定不是静止的。因而,物体在某参照系(或参照物)上观察是静止的,那只能说明这个物体的位移运动状态肯定和这个参照系(或参照物)的位移运动状态一致,即它们的位移演化运动是同方位、同速度的。但是,对其它参照系(或参照物)来说,这个所谓的静止物体并不静止,它正在移动。既然宇宙物质都得运动,那肯定都得有动量(惯性)。例如:有一位乘客,他乘坐在一辆正在作匀速直线运动的客车车厢里。由于这时他同整个车厢处在同一个惯性系里(处在同一个惯性运动速度中),所以运动的车厢并没有对他产生任何作用力的干扰,因此他在车厢里可以行动自如,就像在地面行走时一样。这时,如果这位乘客坐在车厢里的一个座位上打瞌睡,对车厢这个惯性参照系来说,这位乘客是静止的,是没有动量的。但是你并不能说,因为这位乘客相对车厢是静止的,是没有位移运动的,所以他整个身体也就没有了动量(惯性力)所具有的物理属性了。之所以不能如此说,道理很简单:因为乘客的“静止”是相对车厢而言的。如果这位乘客乘坐的客车撞上足够能阻止客车前进的障碍物时,车厢的运行状态肯定一下子从高速的匀速直线运行状态跌落到静止状态,这下非把这位乘客身上的“惯性真神”撞出了原形不可。因为这时路面上的行人清楚地看见这位乘客从自己打瞌睡的座位上飞起,并且穿过玻璃已撞碎的前车窗,朝车子行驶的方向继续飞行,最后摔在离车子十几米远的地上。虽然以车厢作参照系观察,这位乘客坐在座位上是静止不动的,但是没用,静止是对车厢而言的,并不是对地球来讲的。所以,在这个事故中,当乘客(物体)失去车厢这个运动状态的惯性系保护时,也就直接进入了地球这个惯性参照系。对地球来讲,乘客和车厢是以同一速度运行的,因此,当车厢受到障碍物的阻挡停下来时,乘客该有的动量(惯性)属性还是要显现出来的。也就是当车祸发生时,客车一下子从高速运动状态急速停下来的瞬间,这位乘客本身在客车上获得的动量(惯性力)必定要遵守动量守恒原则而使他的身体从座位上弹起而飞出去,这就是动量(惯性)的本质,谁能说在任何惯性系内相对惯性参照系是静止的物体就没有惯性(动量)属性了(在这里可以看出,数学是用来计算量化关系中的数值的,不是用来验证这个量化关系是否能成立)。
牛顿经典力学提出了质量守恒概念。质量守恒的意思,就是不管把物体放置在何种参照系里,它原本固有的质量将保持不变。而且质量是物体能获得动量(惯性力)的根源所在,任何物体只要有了质量,它必定就有动量(惯性力)的存在。质量是物体能获得多少动量(惯性)的基数,如果一个物体没有了质量,也就没有能获得动量(惯性)的基数,也就不可能存有动量(惯性力)。
虽然物体最终能获得多大的动量(惯性力)跟它的运动速度有较大的关系,但是不管这个物体能获得多大的动量(惯性力),它的动量(惯性)势能的转换释放必定跟与它发生物理关系的参照物(物体)的运动状态有着直接的关系,也就是与碰撞物体之间的运动方向、运动速度的相对性有关。因此,我们观察到的宇宙中物质的动量(惯性力)的转换释放的量化关系都呈现一定的矢量性和相对性。也因此可以说,物体之间的动量(惯性)转换释放的量化关系是附随物体之间相对运动的演化状态而确立的。比如:有一列火车,车厢中有一个人坐在座位上,那么这个人相对列车来说是没有动量(惯性力)的,是静止的,但是,相对地球来说,他的确在跟随着车厢作快速运动,因此这个人相对地球肯定是有动量(惯性)的。同样的,有一列停在火车站的列车,它相对地球来说是静止的,是没有动量(惯性)的,但是它相对太阳系的其它星体来说肯定是有动量(惯性)的。再比如,有两架超音速战斗机在空中飞行,并且它们的飞行时速已达到每小时2000公里。可想在如此高的飞行速度下,这两架飞机的动量(惯性力)是非常大的,如果这两架飞机迎面相撞的话,后果不堪设想。然而,当两架飞机是同向同速飞行,并令两架飞机慢慢靠拢,如果技术条件允许的话,两架飞机上的飞行员把手伸出座舱在空中相互握手并在两机之间搭建固定的连接架也能相安无事。这些说明了什么?说明物体的动量(惯性)的相对性原理在起作用。
再例如,有个人在一列匀速直线运动的列车车厢内行走,以列车作为参照物,他在列车上的动量(惯性力)就是他的质量乘上他在列车上行走的速度,因此,他在列车这个惯性系上与其他物体发生碰撞时,他的动量就是: 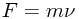 ;当以地球作为参照物时,他在地球这个惯性系上的动量(惯性力)就是他在列车上的行走速度加上列车的运行速度再乘以他身体的质量,此时,与地球上的其他静止物体发生碰撞,他身体的动量就是:
;当以地球作为参照物时,他在地球这个惯性系上的动量(惯性力)就是他在列车上的行走速度加上列车的运行速度再乘以他身体的质量,此时,与地球上的其他静止物体发生碰撞,他身体的动量就是:
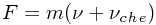 。
。
其实,动量(惯性)的物理性质恰似一位游荡在大自然中的运动健将,在任何运动场合都有他参与的踪影,但由于动量的隐身能力超强,在有些场所不容易被人们察觉到。比如:有一艘匀速直线运动的巨轮,当你在这艘巨轮上打球,不管轮船的航行速度如何,只要保证这艘巨轮的航行是匀速直线运动的,那么,任你怎样用力将球从船头抛向船尾或从船尾抛向船头,球的飞行轨迹和飞行速度与在陆地上打球时一样,并没有任何的差别。也就是说,在船上打球,不管轮船的航行速度的快慢如何,只要轮船能保持匀速直线运动,就不会影响皮球的受力运动轨迹,你在陆地上是如何打球的(无风干扰的环境下打球),在船上也一样如何打球。实质上,这也是动量(惯性)这位“真神”从中成就了如此美事。我们看图八作具体分析:
假如有一个人站在船头的b位置,用力将A球抛向船尾的a点。照理由于人和A球都搭载在这艘匀速直线运动的轮船上,使得人和A球都得到了一个轮船所施加的动量(惯性力),由于这个动量(惯性力)的施力方向与将要抛出的A球的运动方向是相反的,因此,当这个人用力将A球从船头b点抛向船尾a点的一瞬间,A球得到的最终在空中飞行的动量(惯性力)就等于抛投获得的动量(惯性力)减去搭载获得的动量(惯性力)。
用公式表示: 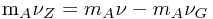
简化后也就是速度相加原理的公式,
即: \(ν_z=ν-ν_G\) ,
也就是说,A球最终在轮船上获得的空中飞行运动速度与在地面上同样受力情况相比,肯定是有差别的,这个差别就是A球最终得到的惯性运动速度比在陆地上同样用力得到的要小。如此,A球也就无法投射到预定的目标a点上,而应该落在a′点上。然而,现实中的情况并非如此。也就是A球的实际落点完全和在陆地上打球时一样,竟落在了预定目标a点上了,这究竟是何道理呢?难道速度相加原理的普适性在这里行不通?非也,其实形成这一结果的道理很简单,因为事件是发生在轮船上的,而我们把这艘正在航行的轮船给忘了。也就是A球的整个飞行过程及下落的预定目标是设立在匀速直线运动的巨轮上的。当A球在空中飞行时,轮船并没有停下来,还是以原来的匀速直线运动状态继续航行。也就是当抛出的A球从空中落到甲板上时,轮船的位置(以船头为基准线)已经从P点移动到Q点,说明A球在空中飞行的同时轮船也移动了一段距离,所以A球不可能落在a′点,而是落在了a点上。同样,当我们用力将B球从船尾抛向船头的这一瞬间, B球也得到了一个惯性力,而这个惯性力(动量)的运动方向是与B球搭载轮船获得的惯性力(动量)的运动方向是同向的,也就是B球最终得到了一个抛投力和惯性力相加的力,
用公式表示: 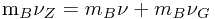 ,
,
简化后成为速度相加公式: 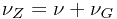 ,
,
照理根据速度相加原理,B球在轮船上得到的惯性运动速度也比陆地上同样得到的要大,也就是B球应该落在b′点的,而不是b点上,但是由于轮船的航行移位使B球落在了b点上。
上述事实说明,力学相对性原理的运作模式完全是依赖于物体的动量(惯性)的演绎模式而构成的,是物体遵守动量守恒而呈现出的一种魔力表现而拥有的。至于力学相对性原理的构成机理,我们就以轮船上的抛投皮球的例子来做个周详地推演。已知,在匀速直线运动的轮船上,就算皮球改为垂直向上抛送,但皮球的最终落点和在陆地上抛球时一样,该落在那儿还落在那儿,这也就是现实中的动量(惯性力)的魔力所在。其中的奥妙在于:当我们把皮球抛在空中时(这个“空中”也是轮船这个“本参照系”的一部分,因为在这个所谓的“空中”弥漫着一种物质——空气,这些空气物质是包裹在船舱中跟随着轮船这个“本参照系”一起移动的,因而在力学相对性原理的架构中,这是个不可或缺的因素之一,如地球的大气层、以及车厢、船舱等相对封闭的空间),由于皮球因搭载轮船而获有的动量(惯性力)在空中得不到很好的、有效的、直接的转换与释放,使得整个皮球在空中飞行时的动量(惯性)守恒效应的动量消耗量正好与轮船的匀速直线运动的位移效应相抵消,这个“相抵消”是力学相对性原理得以实现的关键。可以这样说:在这艘轮船(匀速直线运动参照系)上,由于轮船本身(本参照系)的运动,势必使所有搭载在轮船(本参照系)上的物体产生了一个动量(惯性)效应——均获得了这艘轮船施加的惯性运动动量。而当物体在本参照系内的空域运动时,这个物体在“空域”的“无”动量(惯性)损耗又正好被轮船本身(本参照系)的“匀速直线运动”的航行移动而交接性的校正抵消掉了,以至于船上的乘客打球时感觉不到运动力的改变,就和平时在陆地上打球时的感觉一样。也就是说,在一个匀速直线运动的参照系内,当物体在参照系的空域运动时,由本参照系的运动而产生的动量(惯性)效应恰好能被本参照系的整体移位运动而抵消掉,其结果就是:轮船上的力学原理完全和陆地上的力学原理一样。但是,对地球上的任何运动参照系来讲,要使其参照系内的运动物体的力学原理跟地球上的运动物体的力学原理完全一样,是有一个先决条件的,这个先决条件就是:一定要使该运动参照系保持匀速直线运动状态,否则上述现象不能成立——无法保持力学原理的完整性。因为只有在匀速直线运动的参照系(本参照系)中,才能使在“空域”移动中的物体的动量(惯性)运动状态和本参照系运动的移动状态之间保持平衡并相匹配,也只有这样才能使本参照系的移动量值正好能够抵消掉物体在本参照系空域内的运动而附有的动量(惯性力)守恒效应,也只有这样才能保持力学相对性原理的完整性。
凡持有一定质量的物体,都附有动量(惯性)的存在,因而,在大自然中,到处都可找到动量(惯性)的踪影。比如,物体在绕轴旋转运动时,不光有个向心力,还有个以此相对应的离心力——即“科学上”所认为的向心力的反作用力。不用说,这个离心力也是动量(惯性力)一手造就的。因为根据惯性定义:物体具有保持其原有运动状态的特性。这句话的意思说白了也就是在任何惯性系中,物体在脱离外力影响作用的瞬时,其动量(惯性)一时无法向其它物体转换时将保持守恒——表现为匀速直线运动的状态,这是动量(惯性)的基本属性。因此,物体在旋转运动时也必定有动量(惯性力)的存在,也应该有一个保持匀速直线运动状态的属性,也一定遵守动量(惯性)在物体间的转换法则。
物体在旋转运动时,由于受向心力的作用关系,它的运动方向会不断地发生改变,因而,它所获得的动量(惯性)的运动方向也肯定跟着不断地改变。如此,根据动量(惯性)的守恒定义,可以说,旋转物体一旦脱离向心力的束缚,其动量(惯性)的施力方向必定是沿着物体旋转运动的切线方向运动的。为了便于说明问题,我们可以把旋转运动的物体看成是由许多受力质点组成的,并且每个受力质点应有的匀速直线运动的能力——动量(惯性),肯定是沿切线方向运动的。由这些质点的微小动量(惯性力)的存在,经点滴汇集所获得的沿切线方向运动的动量(惯性力),将以转轴为中心沿切线方向向外排推而形成了一个所谓的离心力。这个离心力在外推的过程中必定会受到一个反作用力(向心力)的作用,这个作用力迫使物体的动量(惯性力)改变运动方向而成为旋转的运动推力。举个雨天撑伞的例子。如果我们在雨天撑伞时,把雨伞旋转起来,伞上的雨水因没有受到雨伞结构的束缚而沿着雨伞旋转圆的切线方向朝四周洒落。在这里如果没有动量(惯性力)的存在,任你雨伞旋转得再快,这些雨水立马还是会从雨伞的边缘直接垂直地落向地面。在这里也可看出,物体在绕轴旋转运动时,其动量(惯性)的方向是朝旋转物体运动轨迹的切线方向运动的。经上述的分析可充分说明,由于动量(惯性)的存在使物体在旋转运动时能获得离心力的根本原因。
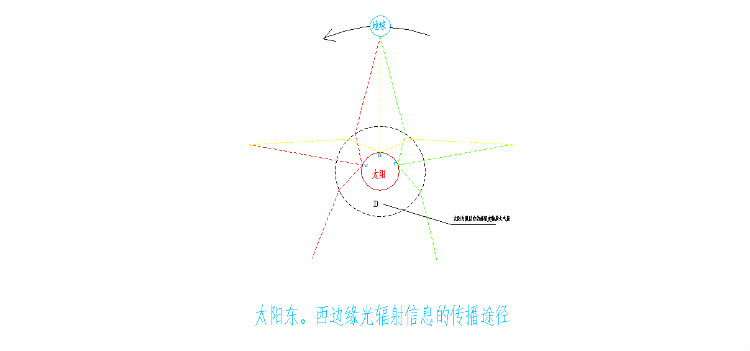
再比如,科里奥利力。科里奥利力实质上也是动量(惯性力)特性的一种隐匿性表现。科里奥利力的现象是由于地球的旋转运动造成的,各位请看附图:
从图中不难看出,由于圆盘(北极点上空俯视地球)的逆时针旋转运动,使得圆盘中的线段,不管你选择哪根线段,以及从线段的哪一头作为始端来思量你在线段上的移位运动,你所前行的正前方方位都在跟随圆盘的逆时针旋转而不停地向左边方向偏移。也就是说,不管你在哪一条线段上,以及从线段的哪一端开始作移位运动的思量,从圆盘(从地球的北极太空空域观看北半球)的上空俯视,你的移位运动方向必然要跟随圆盘(地球的北半球)的旋转节奏而不停地向左边拐弯。出于同样的道理,如果你在地球南半球的话,你在行驶过程中的空域方位应该是不停地向右拐弯。由于动量(惯性力)具有直线运动的特性,因此,当运动物体向左拐弯时,它原本有的动量(惯性力)必定继续保持直线运动状态而呈现出运动物体向右施力的倾向,这样势必造成该运动物体向右倾斜。我想这个向左偏移运动的作用力就是科里奥利力产生的真正原因(在这里有一点要加以说明,由于地球的旋转,使得地球上的物体多多少少附有一些旋转离心力——即目前科学上所称谓的向心力的反作用力,这些旋转离心力附加在科里奥利力上,必定使科里奥利力具有一定的方位性)。关于运动物体在拐弯过程中所呈现出的动量(惯性力)守恒的这一现实效应,我想,乘过交通工具的人或开过汽车的人都颇有心得,用不着我在这里加以细说了。
然而使我费解的是,如此简单的有关科里奥利力的问题,却被当今主流的科学理论搞得非常复杂而高深莫测似的,(如有不信,各位读者可到网上查阅科里奥利力的所谓的科学解释)到末了也没从力学原理的角度解答出在北半球笔直流淌的河流为什么对右岸的冲击较剧,以及火车为什么对右侧轨道的偏压较大的问题所在。我真的不敢相信,这就是人类科学活动所提炼出来的精华?
有人认为:“惯性力和离心力一样,是没有施力物体的,所以从力的要素来看,是不存在这样的力的。 那为什么会出现这种思想概念呢?简单一点讲,就是为了满足牛顿运动定律在非惯性系中的数学表达形式不变而引入的。所谓非惯性系,简单一点讲就是做变速运动的参考系。所以说到底,所谓惯性力和离心力就是在一个加速运动的参考系中观察到的物体惯性的表达形式,是为了计算方便而人为的引入了这样一个概念”。我认为,这种理解好像用错了地方,应该用在力的作用力和反作用力上,而不该用在惯性力上。我有点搞不懂,请问各位,“力”究竟是什么?“力”从哪里来?以及人们为什么会出现如此的惯性力概念?难道在交通工具急刹车或急转弯时,这些人在上面照样行走自如,一点都没感受到惯性力的存在(干扰)?惯性究竟是什么?。其实,作用力和反作用力是动量在转换时体现出的表征,而惯性则是动量守恒时的表象。
最后可能有人要问:在客观现实中,“动量”和“惯性”在用词上是否有区别?这不用问,当然有区别,区别就是:惯性是动量表演出来的,是物体所在参照系的运动方向、运动速度发生改变时把动量“亮”了出来。因此,“动量”是本意,“惯性”是“动量”守恒表演时的用词。
.bmp)

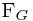 就是物体的质量
就是物体的质量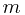 (考虑引力的话这里应该是重力)乘以该物体的运动速度
(考虑引力的话这里应该是重力)乘以该物体的运动速度 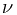 ,
, 。
。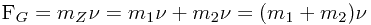 。
。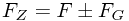 ,
, ,
, 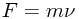 ,
, 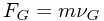 。
。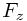 表示炮弹最终得到的动量(惯性力),
表示炮弹最终得到的动量(惯性力), 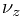 表示同时得到的最终惯性运动速度; 在
表示同时得到的最终惯性运动速度; 在 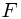 表示炮弹通过弹药这个外力的帮助而得到的惯性运行动量,
表示炮弹通过弹药这个外力的帮助而得到的惯性运行动量, 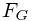 表示炮弹搭载飞机而应有的惯性力(动量),
表示炮弹搭载飞机而应有的惯性力(动量), 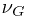 表示搭载而有的惯性运动速度(可以说就是飞机的飞行速度)。
表示搭载而有的惯性运动速度(可以说就是飞机的飞行速度)。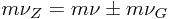
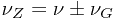 。
。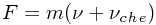 。
。
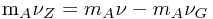
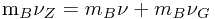 ,
,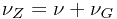 ,
,

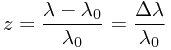
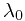 是实验室光源的某一谱线波长,
是实验室光源的某一谱线波长, 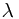 是天体的同一谱线波长。
是天体的同一谱线波长。 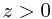 红移,波长增加;
红移,波长增加; 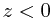 蓝移,波长减少。在红移问题中,z 都大于0,因而往往简单地把 z 作为红移的符号5。哈勃在1929年发现了星系的红移量和距离成正比的规律——哈勃定律。不久,这个哈勃定律就被人们用主观意识所催生的联想,轻易地理解为光(电磁波)的多普勒效应现象——以此感悟出我们的宇宙正在膨胀。我在想,就算光(电磁波)确实存在多普勒效应现象,也不能如此草率地下结论,论为红移就是光(电磁波)的多普勒效应,就是宇宙膨胀的象征。这一说法可要拿出有力的真凭实据来噢!否则无法说服天下人,因为多普勒效应不是这样理解的。下面我们就来探讨一下星系红移与距离成正比的可能因素,以及多普勒效应的真正成因。
蓝移,波长减少。在红移问题中,z 都大于0,因而往往简单地把 z 作为红移的符号5。哈勃在1929年发现了星系的红移量和距离成正比的规律——哈勃定律。不久,这个哈勃定律就被人们用主观意识所催生的联想,轻易地理解为光(电磁波)的多普勒效应现象——以此感悟出我们的宇宙正在膨胀。我在想,就算光(电磁波)确实存在多普勒效应现象,也不能如此草率地下结论,论为红移就是光(电磁波)的多普勒效应,就是宇宙膨胀的象征。这一说法可要拿出有力的真凭实据来噢!否则无法说服天下人,因为多普勒效应不是这样理解的。下面我们就来探讨一下星系红移与距离成正比的可能因素,以及多普勒效应的真正成因。
 表示运动中的观察者所接收到的波长。从图中可以看出,频率的改变就发生在A区域与B区域,与已在空中(介质中)稳定传播的能量波无关,否则不同距离的观察者将听到不同频率的声音,而且运动观察者也不易区分出多普勒效应来。也就是说,当波源运动,观察者静止时,频率的改变只发生在紧靠波源这一端——图中的A区域。这时,整个多普勒效应的物理演绎过程是:波源P‵是在移动中继续不停地发射原有量值的能量波,它一边在发射能量波的同时一边在追赶自身发射出的前一个能量波。而当波源完成一个周波的激发过程时,波源已从P位置移位到P`位置,与波源静止时相比,这个能量周波所涵盖的实际跨越空间(波长
表示运动中的观察者所接收到的波长。从图中可以看出,频率的改变就发生在A区域与B区域,与已在空中(介质中)稳定传播的能量波无关,否则不同距离的观察者将听到不同频率的声音,而且运动观察者也不易区分出多普勒效应来。也就是说,当波源运动,观察者静止时,频率的改变只发生在紧靠波源这一端——图中的A区域。这时,整个多普勒效应的物理演绎过程是:波源P‵是在移动中继续不停地发射原有量值的能量波,它一边在发射能量波的同时一边在追赶自身发射出的前一个能量波。而当波源完成一个周波的激发过程时,波源已从P位置移位到P`位置,与波源静止时相比,这个能量周波所涵盖的实际跨越空间(波长 
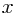 和波源移动速度
和波源移动速度 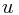 与所发射的辐射波的波速
与所发射的辐射波的波速 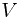 之间的比值有关,用公式表示:
之间的比值有关,用公式表示: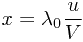 ,
,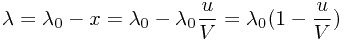 。
。
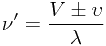
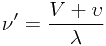
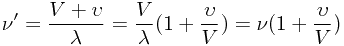 6。
6。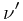 表示运动中的观察者接收到的能量波频率;
表示运动中的观察者接收到的能量波频率; 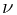 表示静止不动的观察者接收到的原有频率——已经稳定地在介质中传播的能量波频率。
表示静止不动的观察者接收到的原有频率——已经稳定地在介质中传播的能量波频率。